Life at Low Reynolds Number
At small scale momentum is negligible and swimming is hard
The world looks different when you get to the scale on which cells operate. Physical intuition for the large scale does not work on the small scale, and so we have to resort to math to understand movement on the small scale. This is based off a talk that was given by E. M Purcell in 1973, then published in various forms over the next few years. The reference I’m using is the American Journal of Physics vol 45, pages 3-11, 1977.
Viscosity and Fluid dynamics
Viscosity is simply a property of a fluid. Water has a very low viscosity - if you drop a rock into water it will quickly sink. Thick oil has a much higher viscosity - the rock will still sink, but more slowly.
Viscosity creates two regimes of fluid dynamics. At high viscosity, all motions are damped and fluid flow is smooth and constant. At low viscosity, motions are undamped, inertia dominates and fluid flow is chaotic and turbulent.
Which regime you are in depends on more than the viscosity of the fluid - the flow speed, scale and density of the system also matter. This leads us to Reynold’s number (Re). Reynold’s number is defined as the ratio of inertial forces to viscous forces1 and is a way to tell if movement in your system is dominated by inertia or viscosity. A clever derivation2 gives us a simple way to calculate Re:
Where ρ is the density of the fluid, u is the fluid flow speed, μ is the viscosity and L is the characteristic dimension, effectively the scale on which you’re working. The two terms that depend on the fluid are ρ & μ, and for water ρ/μ is about 0.01 cm^2/second. Therefore the Re for an object moving through water scales directly with the size of the object and how fast it is going.
This should make intuitive sense - bigger, faster objects care more about inertia and less about viscosity. Blue whales are very big3 and it makes sense they are less effected by viscous drag than swimming people are. In water the blue whale Re~4x10^8, while Re for a swimming human is about 4x10^64. This means a human needs to exert more continuous effort to keep moving, because viscous drag slows them down more proportionally than it does a whale.
As we keep going down in scale, this process continues. An extremely small fish in water may have an Re between 1-10, and it will quickly slow to a halt unless it is continually swimming.
What is the Reynold’s number of a cell?
This effect is extreme on the scale of a cell. Most bacterial cells are about a micron across and swim around at about 20 microns/second5. Thus, the Re of a typical bacterial cell in water is around 10^-4. If they stop swimming, inertia will carry them 0.1 angstroms, or 10^-5 of their size. Because of the tiny dimensions and (relatively!) slow speed of these cells, they are effectively without momentum.
It’s difficult to understand the implications of not having inertia. The example Purcell uses is to imagine a person trying to swim through a pool of molasses without being able to move any part of their body faster than 1 cm/minute. They can’t build up any inertia to break through the viscosity of the molasses, and are well and truly stuck.
This gets weirder - if you throw out inertia, time stops mattering. The only thing that matters to your current velocity is your current force, and all past forces are irrelevant. Acceleration is instantaneous, and swimming requires specialized movements.
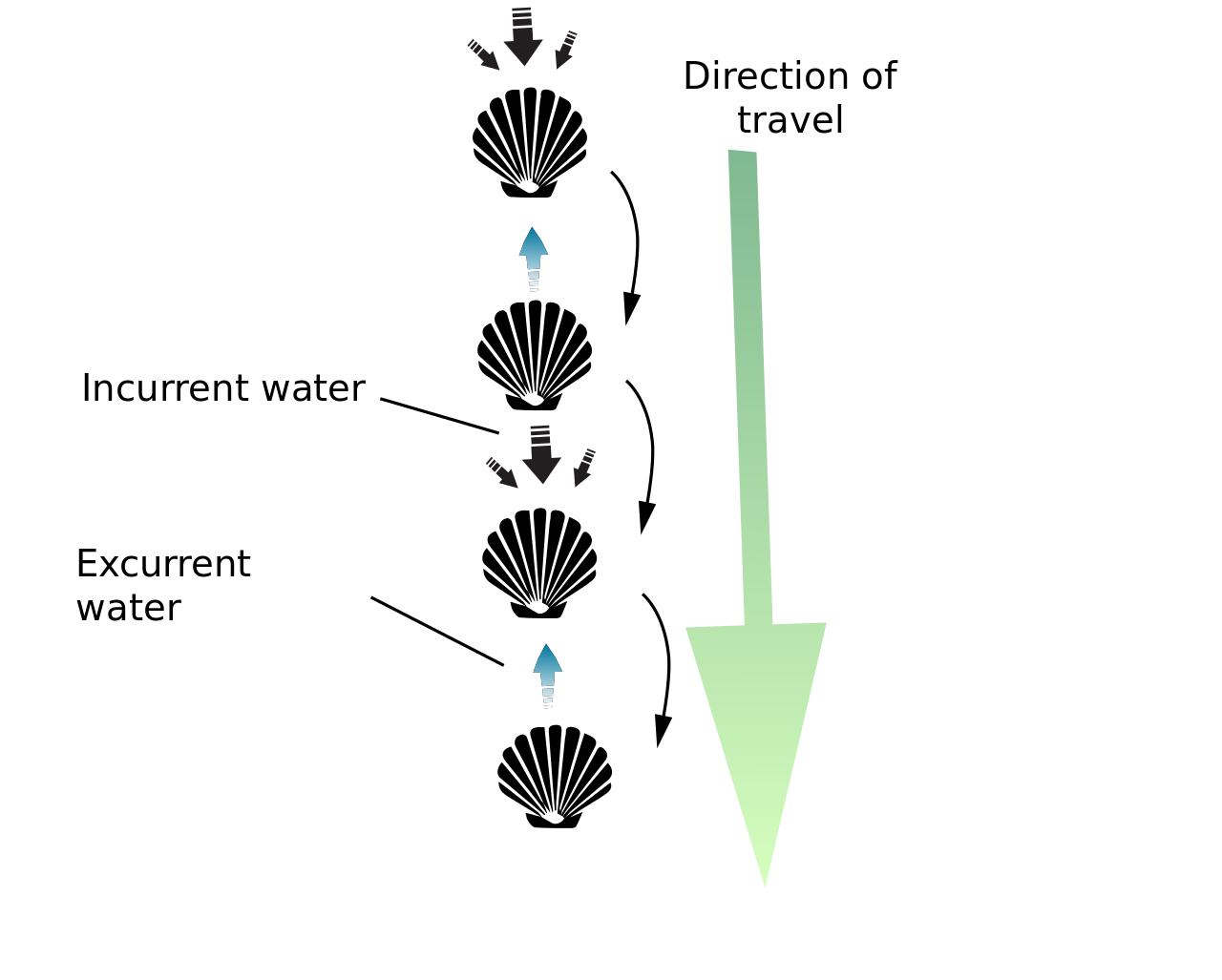
To illustrate this, consider a swimming scallop. It jets along by slowly opening it’s shell to draw in water, then quickly closing it to expel water, building up inertia to make progress.
Figure credit6
This movement would get the scallop nowhere at low Re - the opening motion would pull it backward just as far as closing pushes it forward. We can extend this principle to say that swimming at low Re cannot be reciprocal. It must be a non-time-reversible change of configurations where the motion is different backwards and forwards. The standard swim kick just jackknifes you in the water, it doesn’t make you go anywhere. This is sometimes referred to as the “Scallop Theorem”.
How do you swim at low Re?
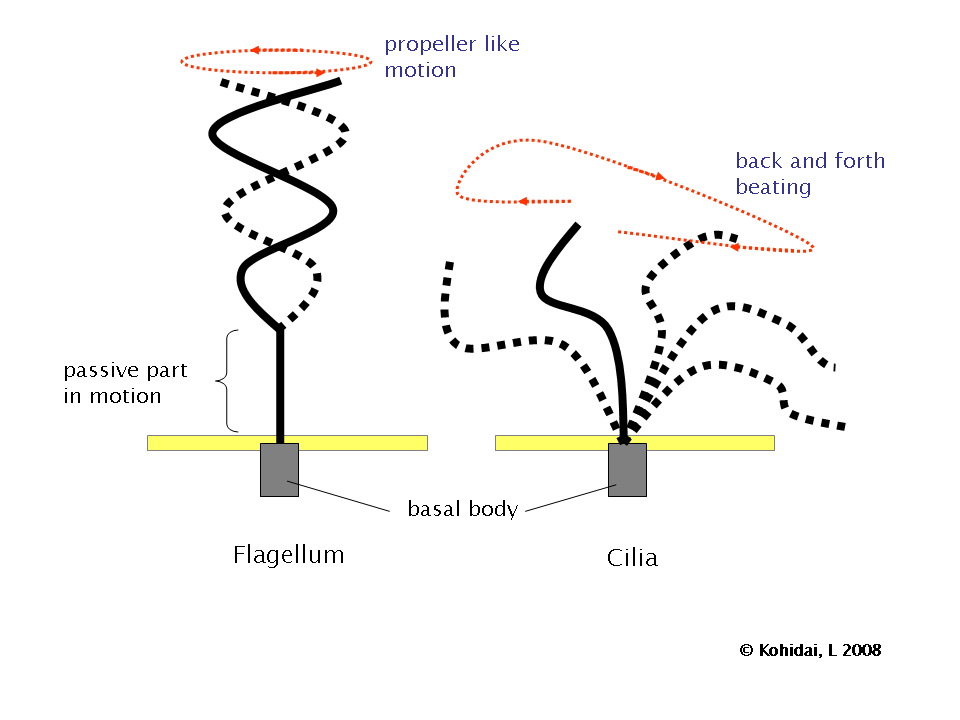
But, cells still swim, and do it pretty well. How? There are two primary solutions to the Scallop theorem.
Figure credit7.
First, a circular motion is non-reversible. So if you attach a flexible filament to a rotational motor you get a flagellum, a propeller-like structure that can push against liquid to move at low Re. Unfortunately, our intuition of propellers isn’t very useful here, since a flagella at low Re doesn’t create a backwards jet of fluid like a large-scale propeller does. Instead it slides itself through the liquid more like a screw into wood, though with a lot more slipping.
Second, a cilia uses a back-and-forth beating motion with a flexible filament. This is non-reversible, as the filament bends one way during the first half of a stroke and the other way during the second half of the stroke. This bending motion pushes against the liquid to provide forward force, though most of the force is sideways and reciprocal.
Both of these approaches have evolved multiple times across biology, and are used by nearly every organism from bacteria to human white blood cells. They’re not necessarily energy-efficient, with Purcell’s calculations estimating that about 1% of the energy that goes into these systems results in forward motion. But overall this is very little energy compared to the energetic cost of continually synthesizing proteins, lipids and nucleic acids.
Out-swimming diffusion
How fast do bacteria have to swim for it to be useful? What do they gain from swimming?
It makes sense that swimming would let you gather more nutrients, in that you’re covering more area and finding more nutrients. But diffusion on the scale of a single cell is fast. To increase the amount of nutrients a cell can absorb would require really high speeds - Purcell calculated out that a cell in a uniform field of nutrients would have to move 700 microns/second to increase the available nutrients 10% (see page 10 for his calculations). That’s more than ten times as fast as bacteria are capable of swimming.
But what if the field of nutrients isn’t uniform? How far do you have to go to see a reasonable change in nutrient conversation? If you can go in a straight line for a while you’ll outrun individual molecules because diffusing molecules are not fast at going long distances, because they turn around and double back a lot. To diffuse a distance l, a molecule takes time t = l^2/D, where D is the diffusion constant. Diffusion velocity over a distance l is therefore v = l/t = D/l. Notice that the equation for velocity is divided by distance - diffusion is slower over longer distances because diffusive motion includes a lot of doubling back.
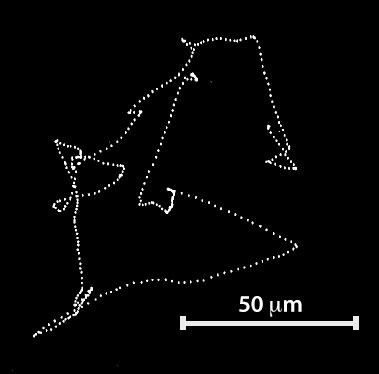
The diffusion constant for glucose in water is about 600 microns^2/second8. So if a cell moves at 20 microns/second, it moves faster than diffusion at distances of 600/20 = 30 microns and over. That’s how far you have to go in a straight line to escape your local diffusion environment.
Here’s a classic diagram of an E. coli swimming from Howard Berg’s website. You’ll notice it goes about 30-50 microns on most of the straight-line paths.
Figure credit9
If you’re more interested in how bacteria do chemotaxis, you can find a few sources explaining how they do a ‘directed random walk’ to move towards higher nutrient concentrations.10
https://en.wikipedia.org/wiki/Reynolds_number
https://en.wikipedia.org/wiki/Reynolds_number#Derivation
https://ocean.si.edu/ocean-life/marine-mammals/what-largest-whale-cetacea-size-comparison-chart
https://en.wikipedia.org/wiki/Reynolds_number#Similarity_of_flows
https://bionumbers.hms.harvard.edu/bionumber.aspx?id=115616&ver=0&trm=E.+coli+speed&org=
By KDS444 - Own work, CC BY-SA 4.0, https://commons.wikimedia.org/w/index.php?curid=34687717
By Kohidai, L. - Own work, CC BY 3.0, https://commons.wikimedia.org/w/index.php?curid=3874754
https://bionumbers.hms.harvard.edu/bionumber.aspx?id=104089&ver=7
http://www.rowland.harvard.edu/labs/bacteria/index.php
https://www.cell.com/current-biology/pdf/S0960-9822(02)01424-0.pdf


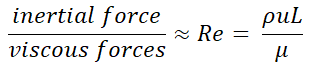
Nice post!
minor typo:
"The diffusion constant for glucose in water is about 600 microns/second"
should be micron^2/second